מצאו את משוואת המעגל החוסם של המשולש עם הקודקודים

Gilad · 3 בספטמבר,‏ 2021,‏ 8:31pm

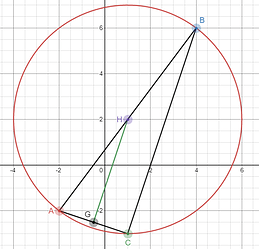
נסמן ב-O להיות מרכז המעגל שחוסם את המשולש הנתון בשאלה.
המפתח לפתור את התרגיל הוא להשתמש במשפט הבא:

משפט: מפגש האנכים האמצעיים במשולש הוא מרכז המעגל החוסם את המשולש.

כזכור, אנך אמצעי הוא ישר המאונך לקטע נתון וחוצה אותו.
לכן כדי לפתור את התרגיל, נמצא את נקודת האמצע (נסמנה ב-H) של אחת הצלעות (למשל AB) ואת שיפוע הישר. מאחר ו-OH הוא אנך אמצעי נובע כי הוא מאונך ל-AB ולכן נוכל לחשב את השיפוע של m_{OH} ולבנות את משוואת הישר OH. באותו אופן, נמצא את נקודת האמצע (נסמנה ב-G) של אחת הצלעות (למשל AC) ואת שיפוע הישר. מאחר ו-OG הוא אנך אמצעי נובע כי הוא מאונך ל-AC ולכן נוכל לחשב את השיפוע של m_{OG} ולבנות את משוואת הישר OG. בעזרת שתי משואות הישר (OH ו-OG) נוכל למצוא את הנקודה O. לאחר מכאן, נוכל לחשב את הרדיוס שמהווה אורך הקטע OC, למשל. בעזרת הנקודה O והרדיוס, נוכל לבנות את משוואת המעגל.

כעת, נבצע את המעברים הטכניים. נסמן ב-H את נקודת האמצע של הקטע AB. נמצא נקודות זו:

\begin{align*} & x_H=\frac{x_A+x_B}{2}=\frac{-2+4}{2}=1\\ & y_H=\frac{y_A+y_B}{2}=\frac{-2+6}{2}=2 \end{align*}

קיבלנו H(1,2). נמצא את השיפוע m_{AB}:

m_{AB}=\frac{6-(-2)}{4-(-2)}=\frac{4}{3}

מאחר והקטע OH הוא אנך אמצעי לישר AB נובע כי הוא מאונך לו ולכן מתקיים:

m_{AB}\cdot m_{OH}=-1\Rightarrow m_{OH}=-\frac{3}{4}

נמצא את משוואת הישר OH:

y-2=-\frac{3}{4}(x-1) \Rightarrow y=-\frac{3}{4}x+\frac{11}{4}

כעת, נבצע אותו דבר על הקטע AC. נסמן ב-G את נקודת האמצע של הקטע AC. נמצא נקודות זו:

\begin{align*} & x_G=\frac{x_A+x_C}{2}=\frac{-2+1}{2}=-0.5\\ & y_G=\frac{y_A+y_C}{2}=\frac{-2+(-3)}{2}=-2.5 \end{align*}

קיבלנו G(-0.5,-2.5). נמצא את השיפוע m_{AC}:

m_{AC}=\frac{-2.5-(-2)}{-0.5-(-2)}=-\frac{1}{3}

מאחר והקטע OG הוא אנך אמצעי לישר AC נובע כי הוא מאונך לו ולכן מתקיים:

m_{AC}\cdot m_{OG}=-1\Rightarrow m_{OG}=3

נמצא את משוואת הישר OG:

y-2=3(x-1) \Rightarrow y=3x-1

כעת, נמצא את הנקודה O:

\left\{\begin{matrix} y=3x-1\\ y=-\frac{3}{4}x+\frac{11}{4} \end{matrix}\right.\Rightarrow O(1,2)

הערה: שים לב כי קיבלנו כי הנקודה O היא באמצע הנקודה H.
כעת, נמצא את הרדיוס. לשם כך, נחשב את אורך OG:

OG=\sqrt{(1-1)^2+(2-(-3))^2}=\sqrt{25}

לכן, משוואת המעגל הינה:

(x-1)^2+(y-2)^2=25

הערה: דרך נוספת לפתור זאת (במקרה ספיציפי זה) היא לשים לב כי מתקיים:

m_{AB}\cdot m_{BC}=-\frac{1}{3}\cdot3=-1

מכך נובע כי הצלע AB מאונכת לצלע BC ולכן לפי משפט AB הוא יתר המעגל שחוסם את המשולש ABC.

למען שלמות התרגיל, אוסיף תרשים של המשולש והמעגל: