הוכיחו כי השטח של המעגל החסום בתוך משולש ישר זווית שבו אורך ניצב אחד הוא 3 ס"מ, אורך ניצב שני הוא 4 ס"מ ואורך היתר הוא 5 ס"מ, הוא בדיוק פאי.
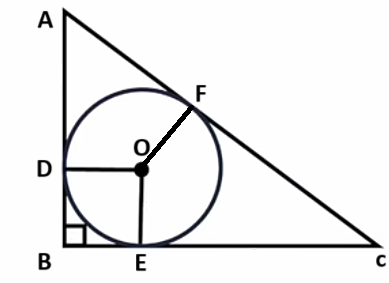
נגדיר משולש 3-4-5 ישר זווית \triangle ABC (נניח כי AB=3cm, BC=4cm ו-AC=5cm) ומעגל עם מרכז O שחסום במשולש זה. נוריד גבהים ממרכז המעגל O לצלעות המשולש כך שנקבל את הצלעות DO, EO ו-FO.
שרטוט:
נסמן את רדיוס המעגל להיות r. הצלעות EO, FO ו-DO הם רדיוסי המעגל ולכן נקבל:
DO=EO=FO=r
משיק למעגל מאונך לרדיוס בנקודת ההשקה ולכן EO\bot BC, DO\bot AB ו-FO\bot AC. מכך נובע כי מרובע \square BDOE הוא ריבוע. אי-לכך, נוכל להסיק כי מתקיים:
BD=BE=DO=EO=r
נתון כי אורך הצלע AC הוא 3 ס"מ ואורך הצלע BC הוא 4 ס"מ. לכן, ע"פ חיסור צלעות נקבל AD=3-r ו-CE=4-r.
שני משיקים למעגל היוצאים מאותה נקודה שווים זה לזה. לכן AF=AD=3-r וגם CF=CE=4-r. נתון כי אורך הצלע AC הוא 5 ס"מ ולכן מחיבור צלעות נקבל:
5=(3-r)+(4-r)\Leftrightarrow r=1cm
קיבלנו כי אורך הרדיוס של המעגל הוא 1 ס"מ. ידוע כי שטח המעגל הוא \pi r^2. ולכן במקרה שלנו נקבל כי שטח המעגל הוא בדיוק \pi.