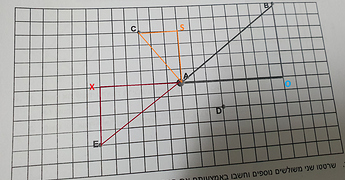
א.נסמן את נקודת מפגש הניצבים של משולש הישר זווית ב-O. נשים לב כי אורך BO הוא 6 יחידות אורך ואילו אורך AO הוא 8 יחידות אורך. לכן בעזרת משפט פיתגורס נקבל את אורך היתר:
AB^2=6^2+8^2=100\Rightarrow AB=10
ב. תחילה נשרטט את המשולשים:
עתה, נשים לב כי CS=3 ו-AS=4 ולכן נחשב את אורך היתר בעזרת משפט פיתגורס:
AC^2=4^2+3^2=25\Rightarrow AC=5
כמו כן, נשים לב כי מתקיים AX=6 ו-XE=4. לפיכך נוכל לחשב את אורך היתר בעזרת משפט פיתגורס:
AE^2=4^2+6^2=52\Rightarrow AC=\sqrt{52}\approx 7.21
בהצלחה.