מציאת שטח משולש במערכת צירים

marbd · 11 בספטמבר,‏ 2019,‏ 9:43pm

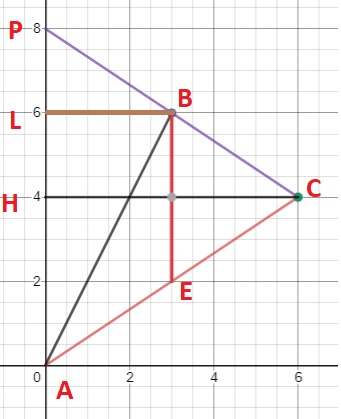
א. עלינו למצוא את הישר AC. תחילה נמצא את השיפוע של הישר:

m=\frac{4-0}{6-0}=\frac{2}{3}

אתה נוכל למצוא את משוואת הישר AC:

y-0=\frac{2}{3}(x-0) \Rightarrow y=\frac{2}{3}x

ידוע כי שיעור ה-x של הנקודה E הוא שיעור ה-x של הנקודה B ולכן x_{E}=3.
נציב במשוואת הישר AC כדי למצוא את השיעור האנכי:

y=\frac{2}{3}\cdot 3=2

קיבלנו כי שיעור הנקודה E הוא (3,2).
ב. נסמן ב-M את נקודת החיתוך של הישר BE עם הציר האופקי. ידוע כי x_{E}=3 ולכן AM=3. כמו כן, נחשב את אורך הצלע BE:

BE=y_{B}-y_{E}=6-2=4

לכן, שטח המשולש AEB הינו:

S_{AEB}=\frac{EB\cdot AM}{2}=\frac{4\cdot 3}{2}=6

כלומר קיבלנו כי שטח המשולש AEB הוא 6 יח"ר.
ג. ישנן מספר דרכים לעשות זאת. הדרך הכי קלה כנראה להמשיך את הישר BC כך שהוא יחצה את הציר האנכי (נסמן את נקודת החיתוך ב-P) ואז לחשב את שטח המשולש PCA ואת שטח הטרפז PBEA ולהחסיר בינהם כדי לקבל את שטח המשולש BCE.
נמצא את הישר BC. לשם כך נחשב את השיפוע של הישר:

m=\frac{6-4}{3-6}=-\frac{2}{3}

לפיכך, משוואת הישר BC הינה:

y-6=-\frac{2}{3}(x-3) \Rightarrow y=-\frac{2}{3}x-8

נמצא את נקודת החיתוך של הישר BC עם הציר האנכי, כלומר את הנקודה P:

y=-\frac{2}{3}\cdot 0+8 =8 \Rightarrow P(0,8)

לכן אורך הצלע AP הוא 8 יחידות.
כדי לחשב את שטח המשולש PCA נוריד גובה מנקודה C לציר האנכי ונסמן אותה ב-H. ידוע כי השיעור האופקי של הנקודה C הוא 6 ולכן CH=6.
סה"כ שטח המשולש PCA הינו:

S_{PCA}=\frac{CH\cdot PC}{2}=\frac{6\cdot 8}{2}=24

עתה, נותר למצוא את שטח הטרפז PBEA. לשם כך, עלינו למצוא את אורך הבסיסים ואת הגובה. אורך BE כבר חישבנו ויצא 4 יחידות. אורך PA גם חישבנו ויצא 8 יחידות. נוריד גובה נקודה B לציר האנכי ונסמן ב-L. ידוע כי השיעור האופקי של הנקודה B הינו 3 ולכן אורך גובה הטרפז BL הינו 3 יחידות. סה"כ נוכל למצוא את שטח הטרפז:

S_{PBEA}=\frac{BL\cdot (BE+AP)}{2}=\frac{3\cdot(8+4)}{2}=18

לכן שטח המשולש BEC המבוקש הינו:

S_{BEC}=S_{APC}-S_{PBEA}=24-18=6

קיבלנו כי שטח המשולש BEC הינו 6 יח"ר.
שרטוט להבנה טובה יותר:

מקווה שברור ומובן