לוויין משוגר אופקית מגובה h מעל הקוטב הצפוני של כדור הארץ. איזו מהירות התחלתית v_0 יש להקנות ללוויין על מנת שמסלולו ישיק לפני כדור הארץ בקוטב הדרומי (ראו שרטוט למעטה)? ניתן להתעלם מסיבוב כדור הארץ סביב צירו.
שרטוט:
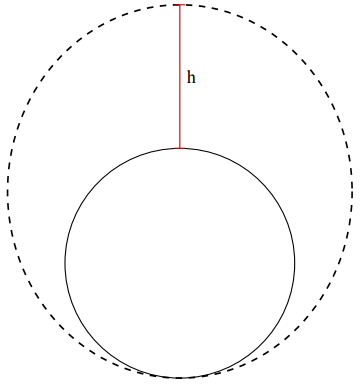
לוויין משוגר אופקית מגובה h מעל הקוטב הצפוני של כדור הארץ. איזו מהירות התחלתית v_0 יש להקנות ללוויין על מנת שמסלולו ישיק לפני כדור הארץ בקוטב הדרומי (ראו שרטוט למעטה)? ניתן להתעלם מסיבוב כדור הארץ סביב צירו.
שרטוט:

תחילה, נמצא את האנרגיה של הלווין בעת השיגור:
נבחר את מישור התנועה להיות מישור xz ולכן התנע הזוויתי הינו:
באופן דומה, בקוטב הדרומי האנרגיה של הלווין הינה:
והתנע הזוויתי הינו:
מחוק שימור תנע זוויתי נקבל:
כמו כן, מחוק שימור אנרגיה נקבל:
נפשט את הביטוי ונעביר אגפים כך שנקבל: