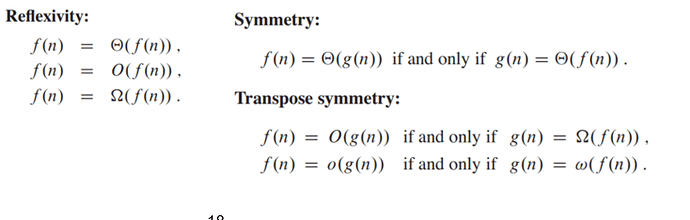שלום לכולם,
אשמח לדעת מה ההבדל בין הטענות האלה?
אלו אינן הוכחות אלא טענות אשר מתבססות על ההגדרות של חסמי סיבוכיות ותורת הקבוצות.
במתמטיקה, יחס בינארי R מעל קבוצה X הוא יחס רפלקסיבי אם עבור כל x\in X, איבר x נמצא ביחס עם עצמו, כלומר מתקיים xRx. לדוגמה יחס השוויון (=) הוא יחס רפלקסיבי שכן לכל a\in X מתקיים a=a.
אחת הטענות שנתונות לך הינה הטענה הבאה: עבור פונקציה f(n) מתקיים f(n)=O(f(n)). כלומר f(n) מהווה חסם עליון אסימפטוטי של עצמה.
ההוכחה של הטענה פשוטה מאוד ומתבססת בעבודה שלכל n מתקיים f(n)\leq f(n). כלומר קיבלנו כי קיימים c=1 ו-n_0=1 כך שלכל n\geq n_{0} מתקיים f(n)\leq c\cdot f(n) ולכן f(n)=O(f(n)) ע"פ ההגדרה.
באותו אופן מוכיחים כי מתקיים f(n)=\Omega(f(n)) . משתי הטענות נקבל f(n)=\Theta(f(n)).
במתמטיקה, יחס בינארי R מעל קבוצה X ייקרא יחס סימטרי כאשר לכל a,b\in X קיום של aRb גורר bRa. לדוגמה יחס השוויון (=) הוא יחס סימטרי שכן לכל a,b\in X, השוויון a=b גורר b=a.
חסמי O ו-\Omega אינם סימטרים. כך לדוגמה, n הוא O(n^2) אבל n^2 הוא לא O(n).
אולם \Theta כן סימטרית ולכן נוכיח זאת.
נהוג להוכיח טענות “אם ורק אם” על-ידי הפרדה לשני כיוונים, אולם נשים לב כי מספיק להוכיח כיוון אחד שכן בכיוון השני פשוט נחליף בין הסימנים.
לכן נוכיח כי אם מתקיים f(n)=\Theta(g(n)) אז בהכרח מתקיים g(n)=\Theta(f(n)).
ע"פ ההגדרה של \Theta קיימים קבועים חיובים שונים c_1,c_2 כך שלכל n\geq n_0 מתקיים:
c_1\cdot g(n)\leq f(n)\leq c_2\cdot g(n)
לכן נקבל g(n)\leq \frac{1}{c_1} \cdot f(n) וגם g(n)\geq \frac{1}{c_2} \cdot f(n). סה"כ נקבל:
\frac{1}{c_2}\cdot f(n)\leq g(n)\leq \frac{1}{c_1}\cdot f(n)
מאחר ו-с_1,c_2 הם קבועים חיוביים נובע כי גם \frac{1}{c_1},\frac{1}{c_2} הם קבועים חיוביים. לכן ע"פ ההגדרה של \Theta נקבל g(n)=\Theta(f(n)), כנדרש.
נותר להוכיח כי חסמי הסיבוכיות מקיימים את סימטרית השחלוף.
נוכיח כי f(n)=O(g(n)) אם"ם g(n)=\Omega (f(n)). נפריד לכיוונים:
-
נניח כי מתקיים f(n)=O(g(n)) ונוכיח כי מתקיים g(n)=\Omega (f(n)). ע"פ ההגדרה של O נוכל להסיק כי קיימים קבועים n_0,c כך שלכל n\geq n_0 מתקיים f(n)\leq c\cdot g(n). לכן נקבל g(n)\geq \frac{1}{c}\cdot f(n). כלומר קיבלנו כי קיימים c'=\frac{1}{c} ו-n_1=n_0 כך שלכל n\geq n_{1} מתקיים g(n)\geq c'\cdot f(n) ולכן g(n)=\Omega(f(n)).
-
נניח כי מתקיים g(n)=\Omega(f(n)) ונוכיח כי מתקיים f(n)=O(g(n)). ע"פ ההגדרה של \Omega נוכל להסיק כי קיימים קבועים n_0,c כך שלכל n\geq n_0 מתקיים g(n)\geq c\cdot f(n). לכן נקבל f(n)\leq \frac{1}{c}\cdot g(n). כלומר קיבלנו כי קיימים c'=\frac{1}{c} ו-n_1=n_0 כך שלכל n\geq n_{1} מתקיים f(n)\leq c'\cdot g(n) ולכן f(n)=O(g(n)).
סה"כ קיבלנו f(n)=O(g(n)) אם"ם g(n)=\Omega (f(n)), כנדרש.
את הטענה הנותרת אני משאיר לך.
מקווה שמובן 
לייק 1