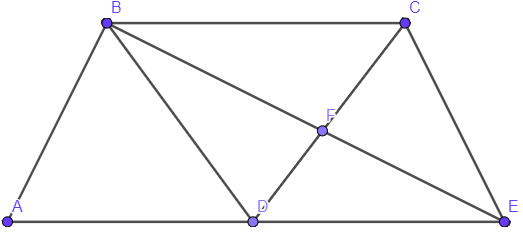
המרובע ABCD הוא מקבילית.
הנקודה F היא אמצע CD, המשך BF חותך את המשך AD בנקודה E.
הוכיחו כי המרובע BCED הוא מקבילית.
שרטוט של מקבילית:
שלום, לא הצלחתי את השאלה הזאת.
תוכלו לעזור לי לפתור אותה?
תודה רבה!
במקבילית הצלעות הנגדיות מקבילות. מרובע ABCD הוא מקבילית ולכן הצלע CD מקביל לצלע AB. הצלע FD הוא מוכל בצלע CD ולכן FD מקביל לצלע AB. לכן ע"פ הרחבה ראשונה של משפט תלס נובע:
\frac{EF}{BE}=\frac{ED}{EA}=\frac{FD}{AB}
נתון כי נקודה F היא אמצע CD ולכן CF=FD. ע"פ חיבור צלעות נקבל CD=2FD. במקבלית הצלעות הנגדיות שוות AB=CD. מכך נקבל AB=2FD.
נציב בשוויון שקיבלנו מתאלס, כך שנקבל:
\frac{EF}{BE}=\frac{FD}{AB}\Rightarrow \frac{EF}{BE}=\frac{FD}{2FD}=\frac{1}{2}
קיבלנו 2EF=BE, כלומר הנקודה F היא אמצע הקטע BE. כמו כן, ע"פ הנתון הנקודה F היא אמצע הקטע CD. סה"כ נוכל להסיק כי האלכסונים חוצים זה את זה במרובע BCED. כל מרובע בו האלכסונים חוצים זה את זה הוא מקבילית ולכן המרובע BCED הוא מקבילית, כנדרש.