שלום לכולם, אני מנסה להוכיח את המשפט הבא:
המשפט: במשולש סכום התיכונים גדול מ-\frac{3}{4} סכום הצלעות, וקטן מסכום הצלעות.
הוכחתי שסכום התיכונים קטן מסכום הצלעות אבל לא הצלחתי להוכיח כי סכום התיכונים גדול מ-\frac{3}{4} סכום הצלעות.
אשמח להכוונה כיצד להוכיח כיוון זה של המשפט.
תודה רבה על העזרה.
נשרטט את המשולש עם שלושת התיכונים:
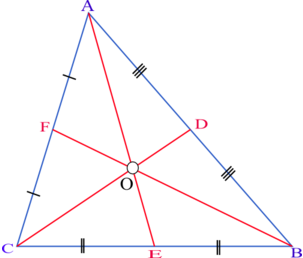
נעזר בכך שמפגש התיכונים מחלק כל תיכון ביחס של 1:2 ונסיק כי מתקיים AO=\frac{2}{3}AE וגם OB=\frac{2}{3}FB. נתבונן על המשולש AOB. בכל משולש, סכום שתי הצלעות גדול מהצלע השלישית ולכן נקבל:
AO+OB>AB
נציב את המשוואות שקיבלנו קודם כך שנקבל:
\frac{2}{3}AE+\frac{2}{3}FB>AB
נעשה את אותו הדבר בשני המשולש AOC ו-COB כך שנקבל את מערכת המשוואות הבאה:
\begin{cases}
\frac{2}{3}AE+\frac{2}{3}FB>AB\\
\frac{2}{3}CD+\frac{2}{3}AE>AC\\
\frac{2}{3}CD+\frac{2}{3}FB>CB
\end{cases}
נחבר את שלושת האי-שוויונים הנ"ל כך שנקבל:
\frac{2}{3}AE+\frac{2}{3}FB+\frac{2}{3}CD+\frac{2}{3}AE+\frac{2}{3}CD+\frac{2}{3}FB>AB+AC+BC
לכן נקבל:
\frac{4}{3}AE+\frac{4}{3}FB+\frac{4}{3}CD>AB+AC+BC
כלומר מתקיים:
AE+FB+CD>\frac{3}{4}\left(AB+AC+BC\right)
כלומר, סכום התיכונים גדול משלושת רבעי סכום הצלעות (היקף המשולש), כנדרש.