לבטא את אורך הקטע במשולש שווה שוקיים בעזרת משפט הסינוסים

מתמטיקה
1

נקודה D נמצאת על הצלע AC של משולש שווה-שוקיים ABC (AB=BC). הצלע AB יוצרת זווית \alpha עם הקטע AD וזווית \beta עם הקטע BD (ראו שרטוט).
נתון כי אורך הקטע DC הוא b.
בטא את אורך הקטע AD באמצעות b, \alpha ו-\beta.
השרטוט:

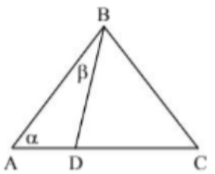
image

אני מבין שצריך להשתמש במשפט הסינוסים אבל אני לא מצליח להבין כיצד.
אשמח להכוונה, תודה רבה.

2

קודם כל נחשב את הזוויות בכל משולש. במשולש שווה שוקיים, זווית הבסיס שוות ולכן \angle A =\angle C=\alpha. במשולש, סכום הזווית שווה ל-180 מעלות ולכן נוכל לחשב את הזווית \angle ADB באופן הבא:

\angle ADB=180^{\circ}-\angle DBA-\angle A=180^{\circ}-\beta-\alpha

הזוויות \angle BDA ו-\angle BDC הן זוויות צמודות ולכן סכומם 180 מעלות. לפיכך נוכל לחשב את הזווית \angle BDC:

\angle BDC=180^{\circ}-\angle BDA=\alpha+\beta

שוב, סכום הזווית במשולש שווה ל-180 מעלות ולכן נוכל לחשב את הזווית \angle DBC:

\angle DBC=180^{\circ}-\angle BDC-\angle C=180^{\circ}-(\alpha+\beta)-\alpha=180^{\circ}-\beta-2\alpha

כעת נשתמש במשפט הסינוסים במשולש BDC כדי לבטא את הצלע BD:

\frac{BD}{\sin\angle C}=\frac{DC}{\sin\angle DBC}

נציב את הנתונים כך שנקבל:

\frac{BD}{\sin(\alpha)}=\frac{b}{\sin(180^{\circ}-\beta-2\alpha)}\Rightarrow BD=\frac{b\sin(\alpha)}{\sin(180^{\circ}-\beta-2\alpha)}

נשתמש בזהות הטרגינומטרית \sin(180^{\circ}-\theta)=\cos\theta כך שנקבל:

BD=\frac{b\sin(\alpha)}{\sin(180^{\circ}-\beta-2\alpha)}=\frac{b\sin(\alpha)}{\cos(\beta+2\alpha)}

כעת נשתמש במשפט הסינוסים במשולש ABD כדי לבטא את הצלע AD:

\frac{AD}{\sin\angle ABD}=\frac{BD}{\sin\angle A}

נציב את הנתונים כך שנקבל:

\frac{AD}{\sin(\beta)}=\frac{b\sin(\alpha)}{\sin(\alpha)\cos(\beta+2\alpha)}=\frac{b}{\cos(\beta+2\alpha)}

לכן נקבל:

AD=\frac{b\sin(\beta)}{\cos(\beta+2\alpha)}