אציע פתרון בעזרת גיאומטריה אנליטית. נמקם את המעגל כך שמרכזו נמצא בראשית מערכת הצירים והצלע DO נמצאת על הציר האופקי כמתואר בשרטוט הבא:
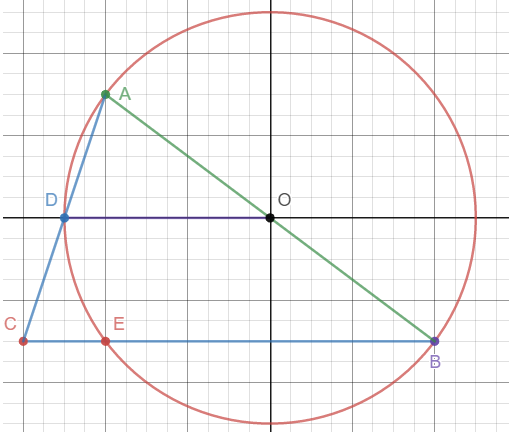
נסמן את רדיוס המעגל ב-R. לכן משוואת המעגל הינה x^2+y^2=R^2. כמו כן, נוכל להסיק כי מתקיים D(-R,0). בנוסף לכך, אורך הצלע AB הוא 2R ולכן עלינו להוכיח כי CB=2R.
נסמן A(x_0,y_0). לכן נקבל B(-x_0,-y_0). לפיכך נוכל להסיק כי משוואת הישר CB הינה y=-y_0. כמו כן, נחשב את השיפוע של הישר AD:
m_{AD}=\frac{y_A-y_D}{x_A-y_D}=\frac{y_0-0}{x_0-R}=\frac{y_0}{x_0-R}
נחשב את משוואת הישר AD (כלומר, AC):
y-0=\frac{y_0}{x_0-R}(x-R)\Rightarrow y=\frac{y_0}{x_0-R}(x-R)
נמצא את נקודת החיתוך של המשוואות AC ו-BC:
\left\{\begin{matrix}
y=\frac{y_0}{x_0-R}(x-R) & \\
y=-y_0 &
\end{matrix}\right. \Rightarrow -y_0=\frac{y_0}{x_0-R}(x-R)\Rightarrow x_C=2R-x_0
לכן, נוכל להסיק כי מתקיים C(2R-x_0,-y_0).
נחשב את אורך הצלע CB:
CB=\sqrt{(2R-x_0+x_0)^2+(-y_0+y_0)^2}=2R
הראנו כי מתקיים CB=AB=2R, כנדרש.