שלום לכולם, די ניתקעתי עם התרגיל הבא:
המרובע ABCD הוא מקבילית. הקטעים DE ו-BF חוצים את הזוויות ADC ו-CBA בהתאמה. הוכיחו כי המרובע EBFD הוא מקבילית.
שרטוט:
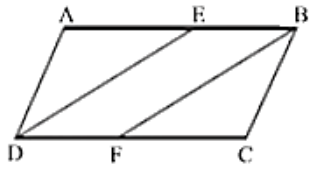
אשמח לעזרה עם התרגיל.
תודה רבה.
כל שתי זוויות נגדיות במקבילית שוות זו לזו ולכן מתקיים \angle D=\angle B. כמו כן, נתון כי הקטעים DE ו-BF חוצים את הזוויות ADC ו-CBA בהתאמה. ולכן בסה"כ נקבל:
\angle ADE=\angle EDF=\angle FBA =\angle FBC
בפרט מתקיים \angle ADE=\angle FBC (ז). כל שתי צלעות נגדיות במקבילית שוות זו לזו ולכן AD=BC (צ). בנוסף לכך, כל שתי זוויות נגדיות במקבילית שוות זו לזו ולכן \angle A=\angle C (ז). סה"כ נקבל כי המשולשים ADE ו-CBF חופפים לפי ז.צ.ז. במשולשים חופפים, הצלעות המתאימות שוות ולכן DE=FB וגם FC=AE. כל שתי צלעות נגדיות במקבילית שוות זו לזו ולכן AB=DC$. מכך שמתקיים FC=AE נקבל ע"פ חיסור זווית EB=DF. סה"כ קיבלנו EB=DF וגם DE=FB. כל מרובע בעל שני זוגות צלעות נגדיות שוות הוא מקבילית ולכן מרובע ABCD הוא מקבילית, כנדרש.
תודה רבה על כל העזרה עם התרגיל הזה! 