מרכז מעגל חסום במשולש

[marbd]

שלום לכולם, אשמח לעזרה עם השאלה הבאה:

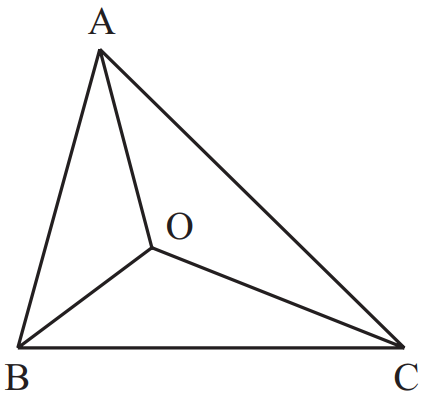
הנקודה O היא מרכז המעגל החסום במשולש ABC.
זוויות המשולש הן \angle BAC=\alpha, \angle ABC=\beta ו-\angle ACB=\gamma.
הוכיחו כי מתקיים:

\frac{S_{\triangle BOC}}{S_{\triangle ABC}}=\frac{\sin\left(\frac{\alpha}{2}\right)}{2\cos\left(\frac{\beta}{2}\right)\cdot\cos\left(\frac{\gamma}{2}\right)}

שרטוט:

מה שאני ניסיתי לעשות: להבנתי, שלושת חוצי הזוויות של משולש נחתכים בנקודה אחת, שהיא מרכז המעגל החסום במשולש. לכן BO, OC ו-AO הם חוצי זווית. כמו כן, אני צריך להשתמש במשפט הסינוסים או משפט הקוסינוסים בכל אחד מהמשולשים אבל משום מה אני לא מצליח להגיע לתשובה הסופית.
אשמח לעזרה, תודה רבה.

[Gilad]

אתה צודק, שלושת חוצי הזוויות של משולש נחתכים בנקודה אחת, שהיא מרכז המעגל החסום במשולש ולכן BO, OC ו-AO הם חוצי זווית. מכך נובע:

\angle BAC=\frac{\alpha}{2}.\,\angle OBC=\frac{\beta}{2},\,\angle OCB=\frac{\gamma}{2}

מחיסור זווית במשולש נקבל \angle AOB=180^{\circ}-0.5\alpha-0.5\beta.
שטח משולש הוא מכפלה של שתי צלעות בסינוס הזווית בינהן, חלקי שתיים ולכן נקבל:

S_{\triangle BOC}=\frac{BO\cdot BC\sin\angle OBC}{2}=\frac{BO\cdot BC\sin\frac{\beta}{2}}{2}

כמו כן מתקיים:

S_{\triangle ABC}=\frac{AB\cdot BC\sin\angle ABC}{2}=\frac{AB\cdot BC\sin\beta}{2}

ע"פ משפט הסינוסים במשולש \triangle ABO נקבל:

\frac{AB}{\sin\angle AOB}=\frac{BO}{\sin\angle BAO}

מכך נוכל להסיק כי מתקיים:

AB=\frac{BO}{\sin\angle BAO} \cdot \sin\angle AOB=BO\cdot \frac{\sin (180^{\circ}-\frac{\alpha}{2}-\frac{\beta}{2})}{\sin\frac{\alpha}{2}}

ע"פ הזהות הטריגונומטרית \sin(180°-\alpha)=\sin(\alpha) נקבל:

AB=BO\cdot \frac{\sin (\frac{\alpha}{2}+\frac{\beta}{2})}{\sin\frac{\alpha}{2}}

לכן נקבל:

\begin{align*} \frac{S_{\triangle BOC}}{S_{\triangle ABC}}&=\frac{BO\cdot BC\sin\frac{\beta}{2}}{2}\cdot\left(\frac{AB\cdot BC\sin\beta}{2}\right)^{-1}\\&=\frac{BO\cdot\sin\frac{\beta}{2}}{AB\cdot\sin\beta}=\frac{BO\cdot\sin\frac{\beta}{2}}{BO\cdot\frac{\sin\left(\frac{\alpha}{2}+\frac{\beta}{2}\right)}{\sin\frac{\alpha}{2}}\cdot\sin\beta}\\&=\frac{\sin\frac{\alpha}{2}\cdot\sin\frac{\beta}{2}}{\sin\beta\cdot\sin\left(\frac{\alpha}{2}+\frac{\beta}{2}\right)}\overset{(1)}{=}\frac{\sin\frac{\alpha}{2}\cdot\sin\frac{\beta}{2}}{\sin\beta\cdot\sin\left(90-\frac{\gamma}{2}\right)}\\&\overset{(2)}{=}\frac{\sin\frac{\alpha}{2}\cdot\sin\frac{\beta}{2}}{\sin\beta\cdot\cos\frac{\gamma}{2}}\overset{(3)}{=}\frac{\sin\frac{\alpha}{2}\cdot\sin\frac{\beta}{2}}{2\sin\frac{\beta}{2}\cos\frac{\beta}{2}\cdot\cos\frac{\gamma}{2}}\\&=\frac{\sin\frac{\alpha}{2}}{2\cos\frac{\beta}{2}\cdot\cos\frac{\gamma}{2}} \end{align*}

הסבר על המעברים:

• מעבר (1) - סכום זוויות במשולש ABC הוא 180 מעלות ולכן \alpha+\beta+\gamma=180. לפיכך נקבל \frac{\alpha}{2}+\frac{\beta}{2}=90-\frac{\gamma}{2}.
• מעבר (2) - לפי הזהות \sin(90^{\circ}-x)=\cos(x).
• מעבר (3) - לפי הזהות \sin x=2\sin\frac{x}{2}\cos\frac{x}{2}.

סה"כ קיבלנו:

\frac{S_{\triangle BOC}}{S_{\triangle ABC}}=\frac{\sin\left(\frac{\alpha}{2}\right)}{2\cos\left(\frac{\beta}{2}\right)\cdot\cos\left(\frac{\gamma}{2}\right)}

כנדרש.