שלום,
אשמח לעזרה עם השאלה הבאה:
צריך לחשב את השטח הכלוא בין הקווים של המשוואה y^2=x+a^2 וציר ה-y באשר a ממשי חיובי כלשהו.
תכלס אין לי מושג איך עושים את זה.
תודה רבה לעוזרים!
היי 
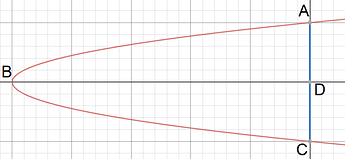
שרטוט של השטח שעלינו לחשב:
עלינו לחשב את השטח הכלוא בין ההיפרבולה y^2=x+a^2 והציר האנכי כאשר 0\leq a\in \mathbb{R}.
אם a=0 אז כמובן השטח שווה לאפס. נחשב את השטח עבור a> 0. מטעמי סימטריה, מספיק לחשב את השטח הכלוא בין ההיפרבולה הנתונה, הציר האופקי והציר האנכי החיובי (כלומר את השטח ABD). תחילה נחשב את הנקודה B:
0^2=x+a^2\Rightarrow x=-a^2\Rightarrow B(-a^2,0)
עתה, נחשב את השטח ABD:
\begin{align*}
\int_{-a^2}^{0}\sqrt{x+a^2}dx&= \left [\frac{2}{3}(x+a^2)^{1.5} \right ]^{0}_{-a^2}= \\ &= \left [\frac{2}{3}(0+a^2)^{1.5} \right ]-\left [\frac{2}{3}(-a^2+a^2)^{1.5} \right ]= \frac{2}{3}a^{3}
\end{align*}
המעבר האחרון נכון בגלל שמתקיים a>0. נכפול ב-2 כדי לקבל את השטח של ABC:
2\cdot S_{ABD}=2\cdot \frac{2}{3}a^{3} = \frac{4}{3}a^{3}
מקווה שהכל מובן 
3 לייקים